For begin

app为什么需要so里面的代码

1
2
执行效率
C/C++反编译比Java难

so中会接触到的：系统库函数、加密算法、jni调用、系统调用、自写算法

so层没有标准加密库调用，无法像Java里那样messageDigest这么明显的识别

Hex编码

Hex 编码的基本步骤

  1. 将数据转换为二进制

    • 每个字符或字节数据用 8 位二进制表示（1 字节 = 8 位）。
    • 例如，字符 'A' 的 ASCII 值是 65，二进制表示为 01000001。

  2. 按 4 位分组

    • 将 8 位二进制分成两个 4 位的部分（每个 4 位称为一个 nibble）。

    • 例如，

      1
      01000001

      分为：

      • 高 4 位：0100
      • 低 4 位：0001

  3. 将每个 4 位二进制转换为十六进制

    • 每 4 位可以表示一个十六进制字符（0-9 和 A-F）。

    • 对于 

      1
      0100

      和 

      1
      0001
      • 0100 → 4
      • 0001 → 1

  4. 组合结果

    • 将两个十六进制字符拼接起来，形成该字节的十六进制表示。
    • 例如，01000001 → 41。

完整示例

假设我们要对字符串 "Hi" 进行 Hex 编码：

步骤 1：获取每个字符的 ASCII 值

  • 'H' → ASCII 值 72 → 二进制 01001000
  • 'i' → ASCII 值 105 → 二进制 01101001

步骤 2：分组并转换为十六进制

  • 'H' 的二进制 01001000：
    • 高 4 位：0100 → 4
    • 低 4 位：1000 → 8
    • Hex 表示：48
  • 'i' 的二进制 01101001：
    • 高 4 位：0110 → 6
    • 低 4 位：1001 → 9
    • Hex 表示：69

步骤 3：组合结果

  • "Hi" 的 Hex 编码结果是：4869

MD5算法

C实现的MD5算法的使用

MD5.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
//
// Created by Administrator on 2021-07-28.
//

#ifndef HOOKDEMO_MD5_H
#define HOOKDEMO_MD5_H

typedef struct {
    unsigned int count[2];
    unsigned int state[4];
    unsigned char buffer[64];
} MD5_CTX;

#define F(x,y,z) ((x & y) | (~x & z))
#define G(x,y,z) ((x & z) | (y & ~z))
#define H(x,y,z) (x^y^z)
#define I(x,y,z) (y ^ (x | ~z))
#define ROTATE_LEFT(x,n) ((x << n) | (x >> (32-n)))
#define FF(a,b,c,d,x,s,ac) \
          { \
          a += F(b,c,d) + x + ac; \
          a = ROTATE_LEFT(a,s); \
          a += b; \
          }
#define GG(a,b,c,d,x,s,ac) \
          { \
          a += G(b,c,d) + x + ac; \
          a = ROTATE_LEFT(a,s); \
          a += b; \
          }
#define HH(a,b,c,d,x,s,ac) \
          { \
          a += H(b,c,d) + x + ac; \
          a = ROTATE_LEFT(a,s); \
          a += b; \
          }
#define II(a,b,c,d,x,s,ac) \
          { \
          a += I(b,c,d) + x + ac; \
          a = ROTATE_LEFT(a,s); \
          a += b; \
          }
void MD5Init(MD5_CTX *context);
void MD5Update(MD5_CTX *context,unsigned char *input,unsigned int inputlen);
void MD5Final(MD5_CTX *context,unsigned char digest[16]);
void MD5Transform(unsigned int state[4],unsigned char block[64]);
void MD5Encode(unsigned char *output,unsigned int *input,unsigned int len);
void MD5Decode(unsigned int *output,unsigned char *input,unsigned int len);

#endif //HOOKDEMO_MD5_H

main.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
//
// Created by Administrator on 2021-07-28.
//
#include <iostream>
#include <memory.h>
#include <string.h>
#include "MD5.h"

using namespace std;

unsigned char PADDING[] = {0x80, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
                           0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
                           0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
                           0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0};

void MD5Init(MD5_CTX *context) {
    context->count[0] = 0;
    context->count[1] = 0;
    context->state[0] = 0x67452301;
    context->state[1] = 0xEFCDAB89;
    context->state[2] = 0x98BADCFE;
    context->state[3] = 0x10325476;
}

void MD5Update(MD5_CTX *context, unsigned char *input, unsigned int inputlen) {
    unsigned int i = 0, index = 0, partlen = 0;
    index = (context->count[0] >> 3) & 0x3F;
    partlen = 64 - index;
    context->count[0] += inputlen << 3;
    if (context->count[0] < (inputlen << 3))
        context->count[1]++;
    context->count[1] += inputlen >> 29;

    if (inputlen >= partlen) {
        memcpy(&context->buffer[index], input, partlen);
        MD5Transform(context->state, context->buffer);
        for (i = partlen; i + 64 <= inputlen; i += 64)
            MD5Transform(context->state, &input[i]);
        index = 0;
    } else {
        i = 0;
    }
    memcpy(&context->buffer[index], &input[i], inputlen - i);
}

void MD5Final(MD5_CTX *context, unsigned char digest[16]) {
    unsigned int index = 0, padlen = 0;
    unsigned char bits[8];
    index = (context->count[0] >> 3) & 0x3F;
    padlen = (index < 56) ? (56 - index) : (120 - index);
    MD5Encode(bits, context->count, 8);
    MD5Update(context, PADDING, padlen);
    MD5Update(context, bits, 8);
    MD5Encode(digest, context->state, 16);
}

void MD5Encode(unsigned char *output, unsigned int *input, unsigned int len) {
    unsigned int i = 0, j = 0;
    while (j < len) {
        output[j] = input[i] & 0xFF;
        output[j + 1] = (input[i] >> 8) & 0xFF;
        output[j + 2] = (input[i] >> 16) & 0xFF;
        output[j + 3] = (input[i] >> 24) & 0xFF;
        i++;
        j += 4;
    }
}

void MD5Decode(unsigned int *output, unsigned char *input, unsigned int len) {
    unsigned int i = 0, j = 0;
    while (j < len) {
        output[i] = (input[j]) |
                    (input[j + 1] << 8) |
                    (input[j + 2] << 16) |
                    (input[j + 3] << 24);
        i++;
        j += 4;
    }
}

void MD5Transform(unsigned int state[4], unsigned char block[64]) {
    unsigned int a = state[0];
    unsigned int b = state[1];
    unsigned int c = state[2];
    unsigned int d = state[3];
    unsigned int x[64];
    MD5Decode(x, block, 64);
    FF(a, b, c, d, x[0], 7, 0xd76aa478); /* 1 */
    FF(d, a, b, c, x[1], 12, 0xe8c7b756); /* 2 */
    FF(c, d, a, b, x[2], 17, 0x242070db); /* 3 */
    FF(b, c, d, a, x[3], 22, 0xc1bdceee); /* 4 */
    FF(a, b, c, d, x[4], 7, 0xf57c0faf); /* 5 */
    FF(d, a, b, c, x[5], 12, 0x4787c62a); /* 6 */
    FF(c, d, a, b, x[6], 17, 0xa8304613); /* 7 */
    FF(b, c, d, a, x[7], 22, 0xfd469501); /* 8 */
    FF(a, b, c, d, x[8], 7, 0x698098d8); /* 9 */
    FF(d, a, b, c, x[9], 12, 0x8b44f7af); /* 10 */
    FF(c, d, a, b, x[10], 17, 0xffff5bb1); /* 11 */
    FF(b, c, d, a, x[11], 22, 0x895cd7be); /* 12 */
    FF(a, b, c, d, x[12], 7, 0x6b901122); /* 13 */
    FF(d, a, b, c, x[13], 12, 0xfd987193); /* 14 */
    FF(c, d, a, b, x[14], 17, 0xa679438e); /* 15 */
    FF(b, c, d, a, x[15], 22, 0x49b40821); /* 16 */

    /* Round 2 */
    GG(a, b, c, d, x[1], 5, 0xf61e2562); /* 17 */
    GG(d, a, b, c, x[6], 9, 0xc040b340); /* 18 */
    GG(c, d, a, b, x[11], 14, 0x265e5a51); /* 19 */
    GG(b, c, d, a, x[0], 20, 0xe9b6c7aa); /* 20 */
    GG(a, b, c, d, x[5], 5, 0xd62f105d); /* 21 */
    GG(d, a, b, c, x[10], 9, 0x2441453); /* 22 */
    GG(c, d, a, b, x[15], 14, 0xd8a1e681); /* 23 */
    GG(b, c, d, a, x[4], 20, 0xe7d3fbc8); /* 24 */
    GG(a, b, c, d, x[9], 5, 0x21e1cde6); /* 25 */
    GG(d, a, b, c, x[14], 9, 0xc33707d6); /* 26 */
    GG(c, d, a, b, x[3], 14, 0xf4d50d87); /* 27 */
    GG(b, c, d, a, x[8], 20, 0x455a14ed); /* 28 */
    GG(a, b, c, d, x[13], 5, 0xa9e3e905); /* 29 */
    GG(d, a, b, c, x[2], 9, 0xfcefa3f8); /* 30 */
    GG(c, d, a, b, x[7], 14, 0x676f02d9); /* 31 */
    GG(b, c, d, a, x[12], 20, 0x8d2a4c8a); /* 32 */

    /* Round 3 */
    HH(a, b, c, d, x[5], 4, 0xfffa3942); /* 33 */
    HH(d, a, b, c, x[8], 11, 0x8771f681); /* 34 */
    HH(c, d, a, b, x[11], 16, 0x6d9d6122); /* 35 */
    HH(b, c, d, a, x[14], 23, 0xfde5380c); /* 36 */
    HH(a, b, c, d, x[1], 4, 0xa4beea44); /* 37 */
    HH(d, a, b, c, x[4], 11, 0x4bdecfa9); /* 38 */
    HH(c, d, a, b, x[7], 16, 0xf6bb4b60); /* 39 */
    HH(b, c, d, a, x[10], 23, 0xbebfbc70); /* 40 */
    HH(a, b, c, d, x[13], 4, 0x289b7ec6); /* 41 */
    HH(d, a, b, c, x[0], 11, 0xeaa127fa); /* 42 */
    HH(c, d, a, b, x[3], 16, 0xd4ef3085); /* 43 */
    HH(b, c, d, a, x[6], 23, 0x4881d05); /* 44 */
    HH(a, b, c, d, x[9], 4, 0xd9d4d039); /* 45 */
    HH(d, a, b, c, x[12], 11, 0xe6db99e5); /* 46 */
    HH(c, d, a, b, x[15], 16, 0x1fa27cf8); /* 47 */
    HH(b, c, d, a, x[2], 23, 0xc4ac5665); /* 48 */

    /* Round 4 */
    II(a, b, c, d, x[0], 6, 0xf4292244); /* 49 */
    II(d, a, b, c, x[7], 10, 0x432aff97); /* 50 */
    II(c, d, a, b, x[14], 15, 0xab9423a7); /* 51 */
    II(b, c, d, a, x[5], 21, 0xfc93a039); /* 52 */
    II(a, b, c, d, x[12], 6, 0x655b59c3); /* 53 */
    II(d, a, b, c, x[3], 10, 0x8f0ccc92); /* 54 */
    II(c, d, a, b, x[10], 15, 0xffeff47d); /* 55 */
    II(b, c, d, a, x[1], 21, 0x85845dd1); /* 56 */
    II(a, b, c, d, x[8], 6, 0x6fa87e4f); /* 57 */
    II(d, a, b, c, x[15], 10, 0xfe2ce6e0); /* 58 */
    II(c, d, a, b, x[6], 15, 0xa3014314); /* 59 */
    II(b, c, d, a, x[13], 21, 0x4e0811a1); /* 60 */
    II(a, b, c, d, x[4], 6, 0xf7537e82); /* 61 */
    II(d, a, b, c, x[11], 10, 0xbd3af235); /* 62 */
    II(c, d, a, b, x[2], 15, 0x2ad7d2bb); /* 63 */
    II(b, c, d, a, x[9], 21, 0xeb86d391); /* 64 */
    state[0] += a;
    state[1] += b;
    state[2] += c;
    state[3] += d;
}

int main(){

//    void MD5Init(MD5_CTX *context);
    MD5_CTX context;
    MD5Init(&context);
//    void MD5Update(MD5_CTX *context,unsigned char *input,unsigned int inputlen);
    unsigned char* plainText = (unsigned char *) "a12345678";
    MD5Update(&context, plainText, strlen(reinterpret_cast<const char *>(plainText)));
//    void MD5Final(MD5_CTX *context,unsigned char digest[16]);
    unsigned char result[16];
    MD5Final(&context, result);

    // MD5 的输出总是 128 位，通常以 32 位十六进制字符串表示，也就是16字节
    // 每个char转换成两位十六进制
    char temp[2] = {0};
    char finalResult[33] = {0};
    for(int i = 0; i < 16; i++){
        int index = i;
        sprintf(temp, "%.2x", result[index]);
        strcat(finalResult, temp);
    }

    cout << finalResult << endl;

    return 0;
}

算法原理

明文的预处理

首先看明文是怎么处理的，即MD5Update(&context, plainText, strlen(reinterpret_cast<const char *>(plainText)));做了什么

步骤1：对明文进行Hex编码

1
xiaojianbang ==> 78 69 61 6f 6a 69 61 6e 62 61 6e 67

步骤2：填充

先把明文填充到448bit，先填充一个1，后面跟对应个数的0（比特位的0）

所以这里明文就会被处理成

1
78 69 61 6f 6a 69 61 6e 62 61 6e 67 80 ...

80就是标志着明文的结束，因为80在二进制层面就是 1000 0000，80的后面一直到448bit的地方就是全0了

再填充64bit的附加消息，用这64bit表示消息长度，如果内容过长，64bit放不下，就取低64bit

注意消息长度要取小端序，比如消息长度是 00 00 00 00 00 00 00 60，转小端序就是 60 00 00 00 00 00 00 00

最终明文处理之后的结果

1
78 69 61 6f 6a 69 61 6e 62 61 6e 67 80 ... 60 00 00 00 00 00 00 00
PS：附加消息

在 MD5 算法中，附加消息的最后 64 位表示的是明文的长度，而不是经过 Hex 编码后的长度。具体来说，它表示的是原始明文的长度（以比特为单位）。

明文长度：指的是原始数据的长度，单位是比特（bit）。例如，字符串 "hello" 中有 5 个字符，每个字符占用 1 字节（8 比特），因此明文长度是：

1
5 字符×8 比特/字符=40 比特

Hex 编码长度：如果将 "hello" 转为 Hex 编码，会变成 "68656c6c6f"，共 10 个字符（每个原始字节用 2 个十六进制字符表示）。
但 MD5 的长度字段只关心原始明文的长度，而不考虑编码后的形式。

如果明文是 “hello”，64 位字段的值是什么？明文 "hello" 的长度是 5 字节，等于 40 比特，64 位字段会存储这个长度（40 比特），并以小端序（little-endian）格式存储。

存储过程：

将 40 转换为 64 位二进制：

1
40 (十进制)=0000000000000000000000000000000000000000000000000000000000101000 (二进制)

按小端序排列（低字节在前，高字节在后）：

1
001010000000000000000000000000000000000000000000000000000000000000101000 00000000 00000000 00000000 00000000 00000000 00000000 000000000010100000000000000000000000000000000000000000000000000000000000

以字节表示：

1
0x28 0x00 0x00 0x00 0x00 0x00 0x00 0x00

MD5的分组长度是512bit，填充位数为1-512bit，如果明文长度刚好为448bit，需要填充512bit，也就是有个512bit的新分组（这个分组由 1 位的 1、447 位的 0 和 64 位的附加消息（表示明文长度） 组成），且附加消息对于每个分组都是一样的，因为代表了明文的长度而不是分组的长度

字节序是字节的顺序不是比特的顺序，单字节不存在字节序

步骤3：明文分块

把处理之后的明文分成16块M1-M16，也就是每块32bit

实际的值 内存中的小端字节序
M1 78 69 61 6f 6f 61 69 78
M2 6a 69 61 6e 6e 61 69 6a
M3 62 61 6e 67 67 6e 61 62
M4 80 00 00 00 00 00 00 80
…
M15 60 00 00 00 00 00 00 60
M16 0 0

步骤4：初始化常量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
typedef struct {
    unsigned int count[2];
    unsigned int state[4]; // 一个int是4字节，也就是8个十六进制
    unsigned char buffer[64];
} MD5_CTX;

void MD5Init(MD5_CTX *context) {
    context->count[0] = 0;
    context->count[1] = 0;
    context->state[0] = 0x67452301;
    context->state[1] = 0xEFCDAB89;
    context->state[2] = 0x98BADCFE;
    context->state[3] = 0x10325476;
}

state[0]到state[4]就是4个初始化常量，注意这里也是以小端序标识的，实际内存中的初始化常量是 01 23 45 67 …

MD5魔改最多的也是这里的初始化常量

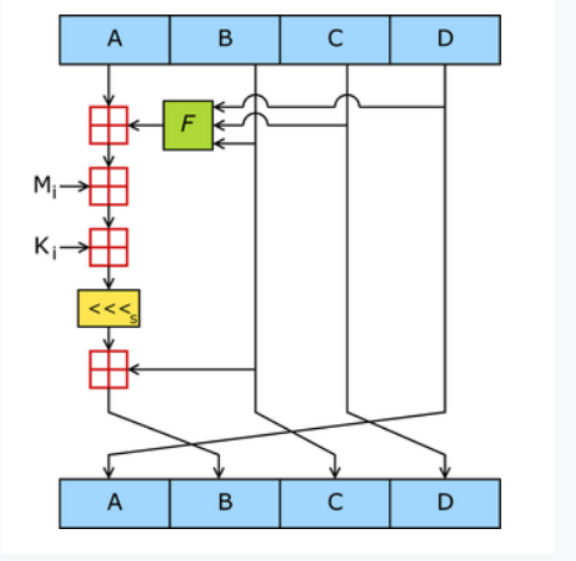
步骤5：MD5Transform

ABCB就是上面的四个初始化的常量，而且图上的转换是一轮，MD5有64轮

每轮都会让旧的ABCD生成新的ABCD，可以看到旧的B给了新的C、旧的C给了新的D、旧的D给了新的A，新的B是旧的A经过一番计算得来的，每轮只计算一个新的B，如果不考虑计算的话，可以简单理解为每轮都把最后的常量提到第一个

Mi就是上面分块的明文，ABCD、F、Ki都是标准MD5算法里规定好的，如果没魔改的话是不变的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
图中的田代表相加
加就是字面意思的加，1+1=2...
上面的过程可以理解为 A + F(B,C,D) + Mi + Ki

图中的F函数并不是一个函数，而是由四个函数构成，每个函数用十六轮，共64轮

K里面代表的值由公式计算，但是体现在代码中一般都是常量,K值可以魔改

<<<s表示循环左移,s代表循环左移的位数，每轮都不一样，但是都是常量，位数一般不会魔改
循环左移，比如二进制 1010 1000 ，循环左移4位，1000 1010 ，相当于往左边移动，移出去的数据往右顶

然后再加上B，得到新的B

最后把四个初始化常量不断变化之后的值，拼接得到最终的摘要结果
1
2
3
4
5
typedef struct {
    unsigned int count[2]; // 代表附加消息，也代表明文的长度，两个int就是8字节，64bit
    unsigned int state[4]; // 一个int是4字节，也就是8个十六进制，代表4个初始化常量
    unsigned char buffer[64]; // 64字节，也就是512bit，代表一个分组
} MD5_CTX;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void MD5Update(MD5_CTX *context, unsigned char *input, unsigned int inputlen) {
    unsigned int i = 0, index = 0, partlen = 0;
    index = (context->count[0] >> 3) & 0x3F; // index是明文的长度
    partlen = 64 - index; // partlen是需要填充的长度
    context->count[0] += inputlen << 3;
    if (context->count[0] < (inputlen << 3))
        context->count[1]++;
    context->count[1] += inputlen >> 29;
    
    if (inputlen >= partlen) {
        memcpy(&context->buffer[index], input, partlen);
        MD5Transform(context->state, context->buffer);
        for (i = partlen; i + 64 <= inputlen; i += 64)
            MD5Transform(context->state, &input[i]);
        index = 0;
    } else {
        i = 0;
    }
    // 如果需要填充的话，暂时不进行填充，后续可能还有数据调用这个方法，知道doFinal里确定没有更多数据了再填充
    memcpy(&context->buffer[index], &input[i], inputlen - i);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 大端序转小端序
---
	int a = 9;
	char * p_a = reinterpret_cast<char *>(&a);
	如果p_a给int *,一次性就访问了四个字节，这里转成char *，可以按字节去访问内存，访问四次就可以依次取出四个字节
---
void MD5Encode(unsigned char *output, unsigned int *input, unsigned int len) {
    unsigned int i = 0, j = 0;
    while (j < len) {
        // input[i]是四个字节，与0xff按位与，就是取最后1个字节
        output[j] = input[i] & 0xFF;
        // input[i]右移8位，再取最后一个字节
        output[j + 1] = (input[i] >> 8) & 0xFF;
        output[j + 2] = (input[i] >> 16) & 0xFF;
        output[j + 3] = (input[i] >> 24) & 0xFF;
        i++;
        j += 4;
    }
}

还有一种字节序转换的方法

1
2
3
char tmp[4] = {0x12,0x34,0x56,0x78};
int *p_a = reinterpret_cast<int *>(&tmp);
这个时候输出*p_a 输出78563412，倒过来了

SHA1算法

SHA1算法的初始化常量有5个，前4个与MD5一致，所以SHA1算法的结果有20字节，结果也是大端序

SHA1算法对于明文的处理与MD5相同，区别是最后的消息长度是大端序

SHA1的分组长度也是512bit，明文也要分段，类似Mi，区别是有80段，后64段是扩展出来的，遵循大端序

SHA1与SHA0的区别就是在扩展这64段的时候，增加了循环左移1位

SHA1的核心计算过程与MD5差不多，区别是K值只有4个，每个K值用20次，总共80轮

SHA1最后计算的结果也是大端序

demo

main.c

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
//
// Created by Administrator on 2021-08-10.
//
#include <string.h>
#include <stdio.h>
#include "md5.h"
#include "sha1.h"

void call_md5() {
//    void MD5Init(MD5_CTX *context);
    MD5_CTX context;
    MD5Init(&context);
//    void MD5Update(MD5_CTX *context,unsigned char *input,unsigned int inputlen);
    unsigned char *plainText = (unsigned char *) "xiaojianbang";
    MD5Update(&context, plainText, strlen(plainText));
//    void MD5Final(MD5_CTX *context,unsigned char digest[16]);
    unsigned char result[16];
    MD5Final(&context, result);

    char temp[2] = {0};
    char finalResult[33] = {0};
    for (int i = 0; i < 16; i++) {
        int index = i;
        sprintf(temp, "%.2x", result[index]);
        strcat(finalResult, temp);
    }
    printf("%s\n", finalResult);
}

void call_sha1() {
    SHA1Context context;
    SHA1Reset(&context);
    unsigned char *plainText = (unsigned char *) "xiaojianbang";
    SHA1Input(&context, plainText, strlen(plainText));
    unsigned char result[16];
    SHA1Result(&context, result);

    char temp[2] = {0};
    char finalResult[41] = {0};
    for (int i = 0; i < 20; i++) {
        int index = i;
        sprintf(temp, "%.2x", result[index]);
        strcat(finalResult, temp);
    }
    printf("%s\n", finalResult);
}

int main() {
    call_md5();
    call_sha1();

    return 0;
}

sha1.c

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
/*
* sha1.c
*
* Description:
* This file implements the Secure Hashing Algorithm 1 as
* defined in FIPS PUB 180-1 published April 17, 1995.
*
* The SHA-1, produces a 160-bit message digest for a given
* data stream. It should take about 2**n steps to find a
* message with the same digest as a given message and
* 2**(n/2) to find any two messages with the same digest,
* when n is the digest size in bits. Therefore, this
* algorithm can serve as a means of providing a
* "fingerprint" for a message.
*
* Portability Issues:
* SHA-1 is defined in terms of 32-bit "words". This code
* uses <stdint.h> (included via "sha1.h" to define 32 and 8
* bit unsigned integer types. If your C compiler does not
* support 32 bit unsigned integers, this code is not
* appropriate.
*
* Caveats:
* SHA-1 is designed to work with messages less than 2^64 bits
* long. Although SHA-1 allows a message digest to be generated
* for messages of any number of bits less than 2^64, this
* implementation only works with messages with a length that is
* a multiple of the size of an 8-bit character.
*
*/
#include <stdio.h>
#include "SHA1.h"

#ifdef __cplusplus
extern "C"
{
#endif

/*
* Define the SHA1 circular left shift macro
*/
#define SHA1CircularShift(bits, word) \
    (((word) << (bits)) | ((word) >> (32-(bits))))

/* Local Function Prototyptes */
void SHA1PadMessage(SHA1Context *);

void SHA1ProcessMessageBlock(SHA1Context *);

/*
* SHA1Reset
*
* Description:
* This function will initialize the SHA1Context in preparation
* for computing a new SHA1 message digest.
*
* Parameters:
* context: [in/out]
* The context to reset.
*
* Returns:
* sha Error Code.
*
*/
int SHA1Reset(SHA1Context *context)//初始化状态
{
    if (!context) {
        return shaNull;
    }
    context->Length_Low = 0;
    context->Length_High = 0;
    context->Message_Block_Index = 0;
    context->Intermediate_Hash[0] = 0x67452301;//取得的HASH结果（中间数据）
    context->Intermediate_Hash[1] = 0xEFCDAB89;
    context->Intermediate_Hash[2] = 0x98BADCFE;
    context->Intermediate_Hash[3] = 0x10325476;
    context->Intermediate_Hash[4] = 0xC3D2E1F0;
    context->Computed = 0;
    context->Corrupted = 0;
    return shaSuccess;
}


/*
* SHA1Result
*
* Description:
* This function will return the 160-bit message digest into the
* Message_Digest array provided by the caller.
* NOTE: The first octet of hash is stored in the 0th element,
* the last octet of hash in the 19th element.
*
* Parameters:
* context: [in/out]
* The context to use to calculate the SHA-1 hash.
* Message_Digest: [out]
* Where the digest is returned.
*
* Returns:
* sha Error Code.
*
*/
int SHA1Result(SHA1Context *context, uint8_t Message_Digest[SHA1HashSize]) {
    int i;
    if (!context || !Message_Digest) {
        return shaNull;
    }
    if (context->Corrupted) {
        return context->Corrupted;
    }
    if (!context->Computed) {
        SHA1PadMessage(context);
        for (i = 0; i < 64; ++i) {
            /* message may be sensitive, clear it out */
            context->Message_Block[i] = 0;
        }
        context->Length_Low = 0; /* and clear length */
        context->Length_High = 0;
        context->Computed = 1;
    }
    printf("%x\n", context->Intermediate_Hash[0]);
    printf("%x\n", context->Intermediate_Hash[1]);
    printf("%x\n", context->Intermediate_Hash[2]);
    printf("%x\n", context->Intermediate_Hash[3]);
    printf("%x\n", context->Intermediate_Hash[4]);

    for (i = 0; i < SHA1HashSize; ++i) {
        Message_Digest[i] = context->Intermediate_Hash[i >> 2]
                >> 8 * (3 - (i & 0x03));
    }
    return shaSuccess;
}


/*
* SHA1Input
*
* Description:
* This function accepts an array of octets as the next portion
* of the message.
*
* Parameters:
* context: [in/out]
* The SHA context to update
* message_array: [in]
* An array of characters representing the next portion of
* the message.
* length: [in]
* The length of the message in message_array
*
* Returns:
* sha Error Code.
*
*/

int SHA1Input(SHA1Context *context, const uint8_t *message_array, unsigned length) {
    if (!length) {
        return shaSuccess;
    }
    if (!context || !message_array) {
        return shaNull;
    }
    if (context->Computed) {
        context->Corrupted = shaStateError;
        return shaStateError;
    }
    if (context->Corrupted) {
        return context->Corrupted;
    }
    while (length-- && !context->Corrupted) {
        context->Message_Block[context->Message_Block_Index++] =
                (*message_array & 0xFF);
        context->Length_Low += 8;
        if (context->Length_Low == 0) {
            context->Length_High++;
            if (context->Length_High == 0) {
                /* Message is too long */
                context->Corrupted = 1;
            }
        }
        if (context->Message_Block_Index == 64) {
            SHA1ProcessMessageBlock(context);
        }
        message_array++;
    }
    return shaSuccess;
}

/*
* SHA1ProcessMessageBlock
*
* Description:
* This function will process the next 512 bits of the message
* stored in the Message_Block array.
*
* Parameters:
* None.
*
* Returns:
* Nothing.
*
* Comments:
* Many of the variable names in this code, especially the
* single character names, were used because those were the
* names used in the publication.
*
*/

void SHA1ProcessMessageBlock(SHA1Context *context) {
    const uint32_t K[] = { /* Constants defined in SHA-1 */
            0x5A827999,
            0x6ED9EBA1,
            0x8F1BBCDC,
            0xCA62C1D6
    };
    int t; /* Loop counter */
    uint32_t temp; /* Temporary word value */
    uint32_t W[80]; /* Word sequence */
    uint32_t A, B, C, D, E; /* Word buffers */
    /*
    * Initialize the first 16 words in the array W
    */
    for (t = 0; t < 16; t++) {
        W[t] = context->Message_Block[t * 4] << 24;
        W[t] |= context->Message_Block[t * 4 + 1] << 16;
        W[t] |= context->Message_Block[t * 4 + 2] << 8;
        W[t] |= context->Message_Block[t * 4 + 3];
    }
    for (t = 16; t < 80; t++) {
        W[t] = SHA1CircularShift(1, W[t - 3] ^ W[t - 8] ^ W[t - 14] ^ W[t - 16]);
        //W[t] = W[t - 3] ^ W[t - 8] ^ W[t - 14] ^ W[t - 16];
    }
    A = context->Intermediate_Hash[0];
    B = context->Intermediate_Hash[1];
    C = context->Intermediate_Hash[2];
    D = context->Intermediate_Hash[3];
    E = context->Intermediate_Hash[4];
    for (t = 0; t < 20; t++) {
        temp = SHA1CircularShift(5, A) +
               ((B & C) | ((~B) & D)) + E + W[t] + K[0];
        E = D;
        D = C;
        C = SHA1CircularShift(30, B);
        B = A;
        A = temp;
    }
    for (t = 20; t < 40; t++) {
        temp = SHA1CircularShift(5, A) + (B ^ C ^ D) + E + W[t] + K[1];
        E = D;
        D = C;
        C = SHA1CircularShift(30, B);
        B = A;
        A = temp;
    }
    for (t = 40; t < 60; t++) {
        temp = SHA1CircularShift(5, A) +
               ((B & C) | (B & D) | (C & D)) + E + W[t] + K[2];
        E = D;
        D = C;
        C = SHA1CircularShift(30, B);
        B = A;
        A = temp;
    }
    for (t = 60; t < 80; t++) {
        temp = SHA1CircularShift(5, A) + (B ^ C ^ D) + E + W[t] + K[3];
        E = D;
        D = C;
        C = SHA1CircularShift(30, B);
        B = A;
        A = temp;
    }
    context->Intermediate_Hash[0] += A;
    context->Intermediate_Hash[1] += B;
    context->Intermediate_Hash[2] += C;
    context->Intermediate_Hash[3] += D;
    context->Intermediate_Hash[4] += E;
    context->Message_Block_Index = 0;
}


/*
* SHA1PadMessage
*
* Description:
* According to the standard, the message must be padded to an even
* 512 bits. The first padding bit must be a ’1’. The last 64
* bits represent the length of the original message. All bits in
* between should be 0. This function will pad the message
* according to those rules by filling the Message_Block array
* accordingly. It will also call the ProcessMessageBlock function
* provided appropriately. When it returns, it can be assumed that
* the message digest has been computed.
*
* Parameters:
* context: [in/out]
* The context to pad
* ProcessMessageBlock: [in]
* The appropriate SHA*ProcessMessageBlock function
* Returns:
* Nothing.
*
*/

void SHA1PadMessage(SHA1Context *context) {
    /*
    * Check to see if the current message block is too small to hold
    * the initial padding bits and length. If so, we will pad the
    * block, process it, and then continue padding into a second
    * block.
    */
    if (context->Message_Block_Index > 55) {
        context->Message_Block[context->Message_Block_Index++] = 0x80;
        while (context->Message_Block_Index < 64) {
            context->Message_Block[context->Message_Block_Index++] = 0;
        }
        SHA1ProcessMessageBlock(context);
        while (context->Message_Block_Index < 56) {
            context->Message_Block[context->Message_Block_Index++] = 0;
        }
    } else {
        context->Message_Block[context->Message_Block_Index++] = 0x80;
        while (context->Message_Block_Index < 56) {
            context->Message_Block[context->Message_Block_Index++] = 0;
        }
    }

    /*
    * Store the message length as the last 8 octets
    */
    context->Message_Block[56] = context->Length_High >> 24;
    context->Message_Block[57] = context->Length_High >> 16;
    context->Message_Block[58] = context->Length_High >> 8;
    context->Message_Block[59] = context->Length_High;
    context->Message_Block[60] = context->Length_Low >> 24;
    context->Message_Block[61] = context->Length_Low >> 16;
    context->Message_Block[62] = context->Length_Low >> 8;
    context->Message_Block[63] = context->Length_Low;
    SHA1ProcessMessageBlock(context);
}


#ifdef __cplusplus
}
#endif

sha1.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
/*
* sha1.h
*
* Description:
* This is the header file for code which implements the Secure
* Hashing Algorithm 1 as defined in FIPS PUB 180-1 published
* April 17, 1995.
*
* Many of the variable names in this code, especially the
* single character names, were used because those were the names
* used in the publication.
*
* Please read the file sha1.c for more information.
*
*/

#ifndef _SHA1_H_
#define _SHA1_H_

#include <stdint.h>
/*
* If you do not have the ISO standard stdint.h header file, then you
* must typdef the following:
* name meaning
* uint32_t unsigned 32 bit integer
* uint8_t unsigned 8 bit integer (i.e., unsigned char)
* int_least16_t integer of >= 16 bits
*
*/
#ifndef _SHA_enum_
#define _SHA_enum_
enum {
    shaSuccess = 0,
    shaNull,         /* Null pointer parameter */
    shaInputTooLong, /* input data too long */
    shaStateError    /* called Input after Result */
};
#endif
#define SHA1HashSize 20
/*
* This structure will hold context information for the SHA-1
* hashing operation
*/
typedef struct SHA1Context {
    uint32_t Intermediate_Hash[SHA1HashSize / 4]; /* Message Digest */
    uint32_t Length_Low; /* Message length in bits */
    uint32_t Length_High; /* Message length in bits */
    /* Index into message block array */
    int_least16_t Message_Block_Index;
    uint8_t Message_Block[64]; /* 512-bit message blocks */
    int Computed; /* Is the digest computed? */
    int Corrupted; /* Is the message digest corrupted? */
} SHA1Context;


/*
* Function Prototypes
*/

int SHA1Reset(SHA1Context *);
int SHA1Input(SHA1Context *, const uint8_t *, unsigned int);
int SHA1Result(SHA1Context *, uint8_t Message_Digest[SHA1HashSize]);

#endif

哈希算法的识别

MD5

初始化常量4个

K表 64个

输出长度16个字节，32个十六进制数，有时候输出16个十六进制数

SHA1

初始化常量5个，前四个和MD5完全相同

K表 4个，每20轮用同一个K作变换，总共80轮

输出长度20字节，40个十六进制数

SHA256

初始化常量8个

K表64个

输出长度32个字节，64个十六进制数

SHA512

初始化常量8个，IDA反编译时有时候显示为16个(字节数解析的问题，8个是8个16字节，解析成16个是被当成8字节每个去解析了)

K表80个

输出长度64字节，128个十六进制数

分组1024bit一组

HmacMD5算法

MAC算法

mac算法其实就是两次加盐，两次hash的一种hash算法

符号含义

1
2
3
4
5
6
7
8
m 明文 
K 原密钥
K' 扩展后的密钥 
ipad 0x36
opad 0x5c
|| 级联，可以理解为就是拼接
H hash函数，如果是HMACSHA1的话这个函数就是SHA1，是HMACMD5的话就是MD5
⨁ 异或

HMAC算法公式
$$
MHAC(K,M) = H((K’⨁opad) || H((K’⨁ipad)||m))
$$
MAC算法也有可能是三次hash，多出来的这一次是针对密钥的，也就是K’和K的关系

如果K比block size大，那么K要进行hash运算得到K’，否则不用

HMACMD5算法步骤

步骤1：密钥扩展

密钥a12345678转Hex编码

1
61 31 32 33 34 35 36 37 38

然后填充0，让密钥长度达到算法的分组长度，MD5的话就是512bit

1
61 31 32 33 34 35 36 37 38 00 ... 00 00

如果密钥太长，就先进行MD5，再填充0，也就是16字节MD5值+一堆0

步骤2：扩展后的密钥与0x36异或

注意0x36也需要扩展到512bit，也就是一堆0x36，cyberchef里会自动扩展，但是代码里需要写

1
57 07 04 05 02 03 00 01 0e 36 36 .. 36 36

步骤3：异或后的数据与明文(message)级联

对应的是上面公式里的 (K'⨁ipad)||m)

1
57 07 04 05 02 03 00 01 0e 36 36 .. 36 36 61 31 32 33 34 35 36 37 38

步骤4：级联后的数据进行hash算法

对应上述的H((K'⨁ipad)||m))

步骤5：扩展之后的密钥与0x5c异或

对应上述的 (K'⨁opad) ，也就是opad之后的数据

步骤6：opad之后的数据与H((K’⨁ipad)||m))之后的数据进行级联

步骤7：步骤6的结果进行hash

得到最终结果

demo

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
key
a12345678

key的Hex形式
61 31 32 33 34 35 36 37 38

扩展到分组长度的key
61313233343536373800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

ipad之后的数据
57070405020300010e36363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636

明文
xiaojianbang

明文的Hex形式
7869616f6a69616e62616e67

ipad之后的数据 和 明文的Hex形式 进行级联
57070405020300010e363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636363636367869616f6a69616e62616e67

级联后的数据 进行一次hash
f573a38d3ea4f054c0b6719c7ab03346

opad之后的数据
3d6d6e6f68696a6b645c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c

opad之后的数据 与hash结果 进行级联
3d6d6e6f68696a6b645c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5c5cf573a38d3ea4f054c0b6719c7ab03346

级联后的数据 进行一次hash
a1cf883260ad4b25f37ae2e572e203d4

代码实现

hmac_md5.h

1
2
3
4
5
6
#ifndef ENCRYPTDEMO_HMAC_MD5_H
#define ENCRYPTDEMO_HMAC_MD5_H

void hmac_md5(unsigned char *out, unsigned char *data, int dlen, unsigned char *key, int klen);

#endif //ENCRYPTDEMO_HMAC_MD5_H

hmac_md5.c

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
#include "hmac_md5.h"
#include "md5.h"

#define LENGTH_MD5_RESULT 16
#define LENGTH_BLOCK 64

void hmac_md5(unsigned char *out, unsigned char *data, int dlen, unsigned char *key, int klen) {
    int i;

    unsigned char tempString16[LENGTH_MD5_RESULT];
    unsigned char OneEnding[LENGTH_BLOCK];
    unsigned char TwoEnding[LENGTH_BLOCK];
    unsigned char ThreeEnding[LENGTH_BLOCK + dlen];
    unsigned char FourEnding[LENGTH_MD5_RESULT];    /*如下步骤四生成的结果*/
    unsigned char FiveEnding[LENGTH_BLOCK];    /*步骤五生成的结果*/
    unsigned char SixEnding[LENGTH_BLOCK + LENGTH_MD5_RESULT];

    char ipad;
    char opad;
    MD5_CTX md5;

    ipad = 0x36;
    opad = 0x5c;

    /*
     * (1) 在密钥key后面添加0来创建一个长为B(64字节)的字符串(OneEnding)。如果key的长度klen大于64字节，则先进行md5运算，使其长度klen=16字节。
     * */

    for (i = 0; i < LENGTH_BLOCK; i++) {
        OneEnding[i] = 0;
    }

    if (klen > LENGTH_BLOCK) {
        MD5Init(&md5);
        MD5Update(&md5, key, klen);
        MD5Final(&md5, tempString16);
        for (i = 0; i < LENGTH_MD5_RESULT; i++)
            OneEnding[i] = tempString16[i];
    } else {
        for (i = 0; i < klen; i++)
            OneEnding[i] = key[i];
    }

    /*
     * (2) 将上一步生成的字符串(OneEnding)与ipad(0x36)做异或运算，形成结果字符串(TwoEnding)。
     * */

    for (i = 0; i < LENGTH_BLOCK; i++) {
        TwoEnding[i] = OneEnding[i] ^ ipad;
    }

    /*
     * (3) 将数据流data附加到第二步的结果字符串(TwoEnding)的末尾。
     * */

    for (i = 0; i < LENGTH_BLOCK; i++) {
        ThreeEnding[i] = TwoEnding[i];
    }
    for (; i < dlen + LENGTH_BLOCK; i++) {
        ThreeEnding[i] = data[i - LENGTH_BLOCK];
    }

    /*
     * (4) 做md5运算于第三步生成的数据流(ThreeEnding)。
     * */

    MD5Init(&md5);
    MD5Update(&md5, ThreeEnding, LENGTH_BLOCK + dlen);
    MD5Final(&md5, FourEnding);

    /*
     * (5) 将第一步生成的字符串(OneEnding)与opad(0x5c)做异或运算，形成结果字符串(FiveEnding)。
     * */

    for (i = 0; i < LENGTH_BLOCK; i++) {
        FiveEnding[i] = OneEnding[i] ^ opad;
    }

    /*
     * (6) 再将第四步的结果(FourEnding)附加到第五步的结果字符串(FiveEnding)的末尾。
     * */

    for (i = 0; i < LENGTH_BLOCK; i++) {
        SixEnding[i] = FiveEnding[i];
    }
    for (; i < (LENGTH_BLOCK + LENGTH_MD5_RESULT); i++) {
        SixEnding[i] = FourEnding[i - LENGTH_BLOCK];
    }

    /*
     * (7) 做md5运算于第六步生成的数据流(SixEnding)，输出最终结果(out)。
     * */

    MD5Init(&md5);
    MD5Update(&md5, SixEnding, LENGTH_BLOCK + LENGTH_MD5_RESULT);
    MD5Final(&md5, out);
}

main.c

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
#include <string.h>
#include <stdio.h>
#include "md5.h"
#include "sha1.h"
#include "sha256.h"
#include "sha512.h"
#include "hmac_md5.h"

void call_md5() {
    MD5_CTX context;
    MD5Init(&context);
    unsigned char *plainText = (unsigned char *) "xiaojianbang";
    MD5Update(&context, plainText, strlen(plainText));
    unsigned char result[16];
    MD5Final(&context, result);

    char temp[2] = {0};
    char finalResult[32] = {0};
    for (int i = 0; i < 16; i++) {
        int index = i;
        sprintf(temp, "%.2x", result[index]);
        strcat(finalResult, temp);
    }
    printf("md5：%s\n", finalResult);
}

void call_sha1() {
    SHA1Context context;
    SHA1Reset(&context);
    unsigned char *plainText = (unsigned char *) "xiaojianbang";
    SHA1Input(&context, plainText, strlen(plainText));
    unsigned char result[20];
    SHA1Result(&context, result);

    char temp[2] = {0};
    char finalResult[40] = {0};
    for (int i = 0; i < 20; i++) {
        int index = i;
        sprintf(temp, "%.2x", result[index]);
        strcat(finalResult, temp);
    }
    printf("sha1：%s\n", finalResult);
}

void call_sha256() {
    SHA256_CTX context;
    sha256_init(&context);
    unsigned char *plainText = (unsigned char *) "xiaojianbang";
    sha256_update(&context, plainText, strlen(plainText));
    unsigned char result[32];
    sha256_final(&context, result);

    char temp[2] = {0};
    char finalResult[64] = {0};
    for (int i = 0; i < 32; i++) {
        int index = i;
        sprintf(temp, "%.2x", result[index]);
        strcat(finalResult, temp);
    }
    printf("sha256：%s\n", finalResult);
}

void call_sha512() {
    SHA512_CB context;
    SHA512Init(&context);
    unsigned char *plainText = (unsigned char *) "xiaojianbang";
    SHA512Update(&context, plainText, strlen(plainText));
    unsigned char result[64];
    SHA512Final(&context, result);

    char temp[2] = {0};
    char finalResult[128] = {0};
    for (int i = 0; i < 64; i++) {
        int index = i;
        sprintf(temp, "%.2x", result[index]);
        strcat(finalResult, temp);
    }
    printf("sha512：%s\n", finalResult);
}

void call_hmac_md5() {
    unsigned char* plainText = (unsigned char *) "xiaojianbang";
    unsigned char* key = (unsigned char *) "a12345678";
    unsigned char result[16];
    hmac_md5(result, plainText, strlen(plainText), (unsigned char *) key, strlen(key));
    char temp[2] = {0};
    char finalResult[32] = {0};
    for (int i = 0; i < 16; i++) {
        int index = i;
        sprintf(temp, "%.2x", result[index]);
        strcat(finalResult, temp);
    }
    printf("hamc_md5：%s\n", finalResult);
}

int main() {
    call_md5();
    call_sha1();
    call_sha256();
    call_sha512();
    call_hmac_md5();
    return 0;
}

算法识别

大部分是hash算法，除了0x36和0x5c这个特征，十进制就是54和92

MD5、魔改的MD5、HmacMD5最后的结果都是16字节