密码学提升-对称加密算法原理及C实现
DES算法
DES算法细节
https://www.anquanke.com/post/id/177808#h3-5
分组加密算法的填充方式
分组大小8字节
明文长度不够1个分组,就需要填充,以最常用的PKCS7填充为例
明文没有内容或者明文刚好一个分组长度,都需要再填充一个分组
最多填充一个分组,08 08 08 08 08 08 08 08
其他填充的情况
1 | ab cd ef ab cd ef ab 01 |
密钥不存在填充,DES必须8字节
子密钥生成
1 | 1. 不考虑填充方式 |
明文:0123456789ABCDEF
密钥:133457799BBCDFF1
把密钥转二进制
1 | 00010011 00110100 01010111 01111001 10011011 10111100 11011111 11110001 |
根据PC1表,对密钥进行重新排列
1 | int PC1_Table[56] = { |
这里的57是指的二进制位的密钥里的第57个(从1开始数不是从0开始数)bit位,也就是1
密钥编排后的结果(这也就是为什么密钥是8字节的,但是有效位数实际上是56位)
1 | 1111000 0110011 0010101 0101111 0101010 1011001 1001111 0001111 |
接下来将这56比特长的密钥分成左右两部分,命名为C0,D0
1 | C0 = 1111000 0110011 0010101 0101111 |
循环左移规定的位数,得到C1,D1到C16,D16的十六个数据,左移的位数根据下面的key_shift表来确定
1 | key_shift = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]; |
C2D2可以对C1D1分别左移1位来得到(注意是1位,key_shift的第二个元素指的是在C1D1的基础上还需要移动的位数),C2D2也可以对C0D0分别左移2位来得到
将C1D1拼接起来,继续后续的处理
1 | C1D1 = 1110000 1100110 0101010 1011111 1010101 0110011 0011110 0011110 |
根据PC2表进行重排,56bit长的CnDn只留下48比特
1 | int PC2_Table[48] = { |
重排后CnDn就是子密钥,命名为Kn
后续DES的十六轮运算中,第n轮就是用Kn,16个子密钥为
1 | K1 = 000110 110000 001011 101111 111111 000111 000001 110010 |
明文的处理
明文的编排
把明文转二进制
1 | 00000001 00100011 01000101 01100111 10001001 10101011 11001101 11101111 |
根据IP表,对明文进行初始置换
1 | int IP_Table[64] = { |
明文重新排列后的结果
1 | 11001100 00000000 11001100 11111111 11110000 10101010 11110000 10101010 |
明文的运算
首先将明文分成左右两半,像上面的密钥一样
L0 和 R0
1 | L0:11001100 00000000 11001100 11111111 |
然后会对L0和R0做16轮迭代
16轮迭代的基本套路
1 | Ln = Rn-1(本轮的L就是上一轮的R) |
以n = 1为例:
1 | L1 = R0 = 11110000 10101010 11110000 10101010 |
F函数的逻辑
f函数传入了R0与K1,即第1个子密钥
1 | R0 = 11110000 10101010 11110000 10101010 |
R0为32bit,K1为48bit,长度不同,没法按位异或
将32bit的R0扩展成48bit,使用到E表
1 | E(R0) = 011110 100001 010101 010101 011110 100001 010101 010101 |
进行密钥混合 E(R0) ^ K1
1 | E(R0) = 011110 100001 010101 010101 011110 100001 010101 010101 |
然后就进入到DES算法核心
也就是S盒,S盒里是8*64个数据,即8个S盒,每个盒都是64个数据
将上一步的结果分成8块6bit
1 | B1 = 011000 |
把B1-B8的值当成索引,在S1-S8盒中取值,规则如下:
以B1为例,值为011000,将它分成0 1100 0,得到
1 | i = 00 即 0 (这里是二进制的00转十进制) |
在S1(因为是B1,所以就在S1里找)中查找第0行第12列的值(这里从0开始算)
1 | int S_Box[8][4][16] = { |
第0行第12列的值为5
1 | B1 = 5 = 0101 |
再以B2为例
1 | B2 = 0 1000 1 |
B1在S1中找,B2在S2中找,以此类推
最后,8个6比特的值在S盒作用下变成8个4比特的值
1 | S(K1+E(R0)) = 0101 1100 1000 0010 1011 0101 1001 0111 |
得到的结果进行P表的重排
1 | int P_Table[32] = { |
1 | P(S(K1+E(R0))) = 0010 0011 0100 1010 1010 1001 1011 1011 |
F函数完事,即F = P(S(K1+E(R0)))
F的结果与L0异或
1 | L1 = R0 = 11110000 10101010 11110000 10101010 |
一轮运算完毕,16轮运算的操作完全一致
1 | L1: 11110000 10101010 11110000 10101010 |
然后,L16和R16倒换,左右调一下顺序,结果为R16L16
1 | R16L16 = 00001010 01001100 11011001 10010101 01000011 01000010 00110010 00110100 |
最后一步,根据FP表进行末置换
1 | 10000101 11101000 00010011 01010100 00001111 00001010 10110100 00000101 |
1 | int FP_Table[64] = { |
上述数据的十六进制形式为
1 | 85 e8 13 54 0f 0a b4 05 |
PS:末置换就是初始置换的逆运算,意思如下
最后这里的FP_Table和一开始的IP_Table是互为可逆的
1 | int IP_Table[64] = { |
demo
1 |
|
DES的魔改
明文的初始置换和末置换,取消或者修改,都不影响DES的安全性
S盒
白盒,AES里比较多,效果就是反编译出了代码也拿不到密钥,密钥的生成在代码中实现,这个得去扣代码或者主动调用
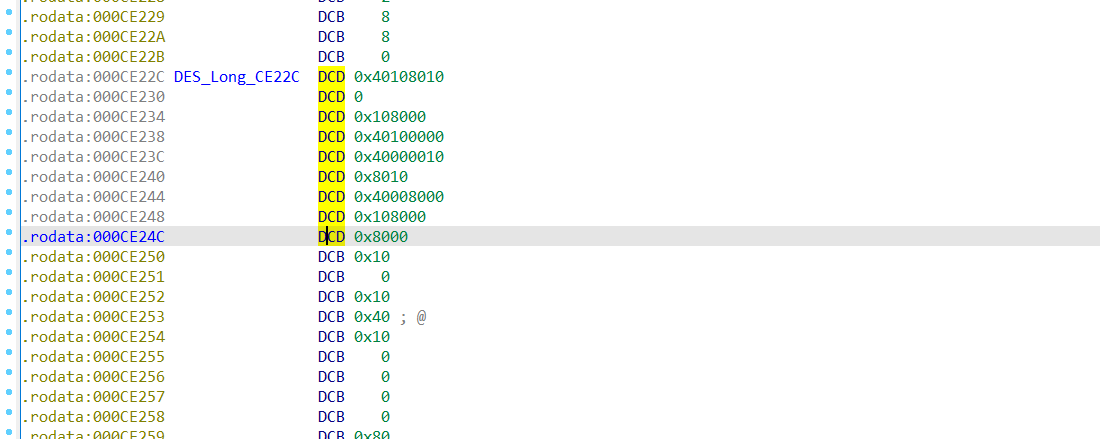
DES的查表法
为了加快加密的速度,在加密结果有限的情况下,有的代码里会把所有可能的加密结果放到一张表里,直接去查这张表
比如libcrypto.so
去搜这个0x40108010就行,可以搜到是DES的,一般是固定的,用于特定场景
分组加密的填充
上面的demo,是没有填充的
明文长度不够1个分组,就需要填充,以最常用的PKCS7填充为例
明文没有内容或者明文刚好一个分组长度,都需要再填充一个分组
最多填充一个分组,08 08 08 08 08 08 08 08 (PKCS7)
其他填充的情况
1 | ab cd ef ab cd ef ab 01 (明文7个字节) |
DES加密的结果一定是分组长度的倍数
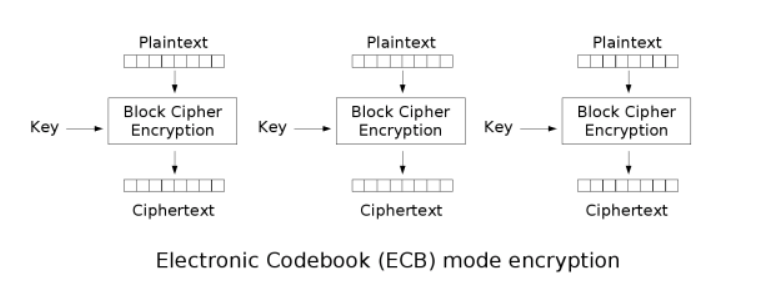
分组加密的模式-ECB
明文超过1个分组长度,就需要了解加密/工作模式
ECB模式,每个分组之间单独加密、互不关联
2个分组明文一样,结果也一样,那么只需要破解其中一个就可以了
可以通过替换某段密文来达到替换明文的目的
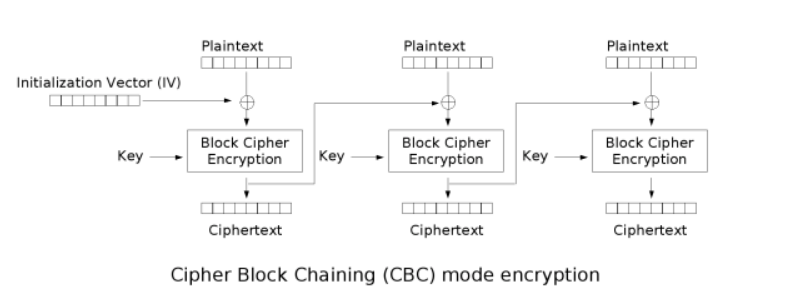
分组加密的模式-CBC
每个明文分组先和上个分组的密文进行异或,得到的结果进行加密得到密文,这里的加密其实就是ECB的加密
第一个明文块没有上个分组的密文块,需要指定一个64bit的输入,也就是初始化向量iv
流程图
CBC模式举例
1 | 明文:123456789ABCDEF0 |
分组加密的模式-CFB
1 | 明文:123456789ABCDEF0 |
分组加密的模式-OFB
1 | 明文:123456789ABCDEF0 |
两个分组的OFB模式
1 | 明文:123456789ABCDEF0 123456789ABCDEF0 |
CFB/OFB都可以作为流加密,可以理解为没有填充
1 | 明文:a1 |
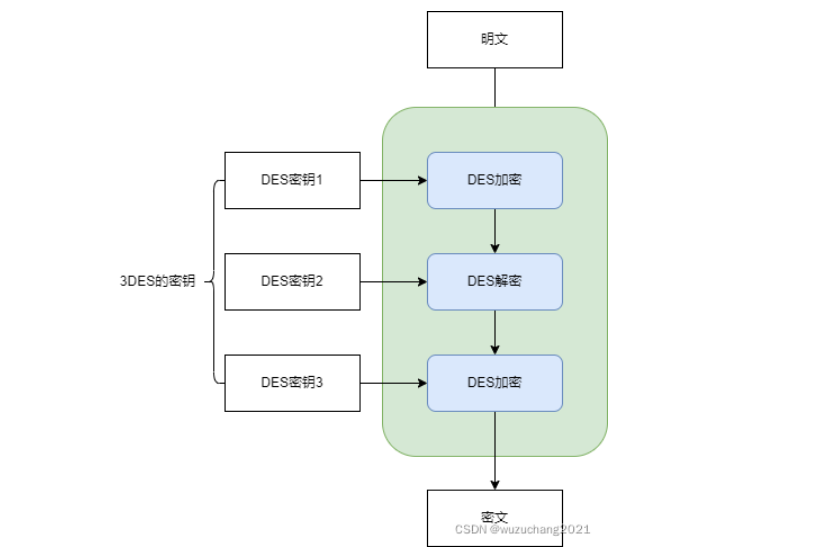
3DES算法
密钥24个字节,等于3个DES的密钥
3DES处理流程,每次使用一个DES密钥
1 | 流程:DES加密->DES解密->DES加密 |
前两个DES密钥相同时,3DES结果等于最后1个密钥DES加密之后的结果
AES算法
特点
1 | 在一个分组长度内,明文的长度变化,AES的加密结果长度都一样,因为有填充 |
Rijndael算法也叫AES算法,Rijndael算法本身分组长度可变,但是定位AES算法之后,分组长度只有128一种
DES中是针对bit进行操作,AES中是针对字节进行操作
AES128是10轮运算、AES192是12轮运算、AES256是14轮运算
明文的运算
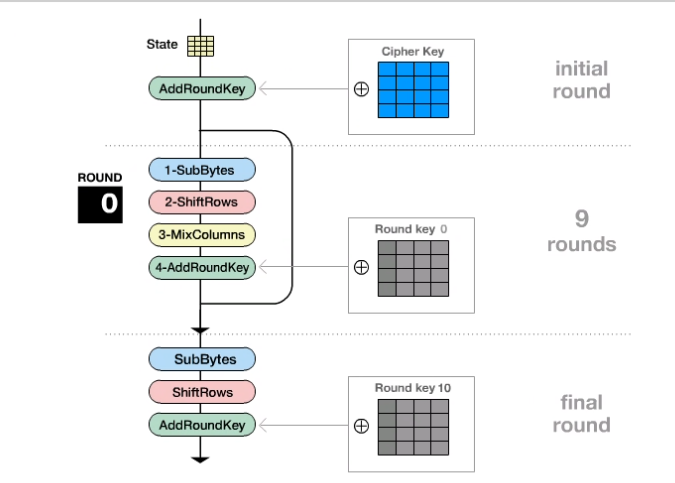
AES整体流程
初始转换
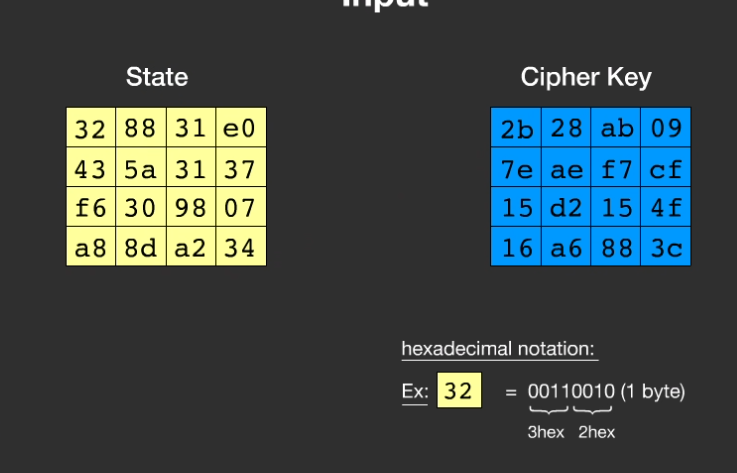
1 | 明文state化(明文和密钥变成4*4的矩阵) |
明文state化
1 | 明文:32 43 f6 a8 88 5a 30 8d 31 31 98 a2 e0 37 07 34 |
明文运算流程(ECB模式,state是明文,如果是CBC模式state会先和iv异或)
1 | 1.AddRoundKey是轮密钥加 |
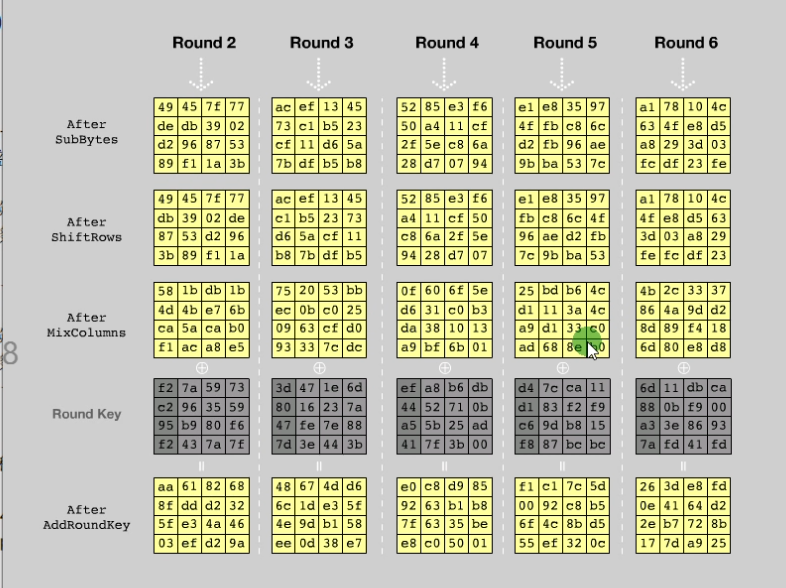
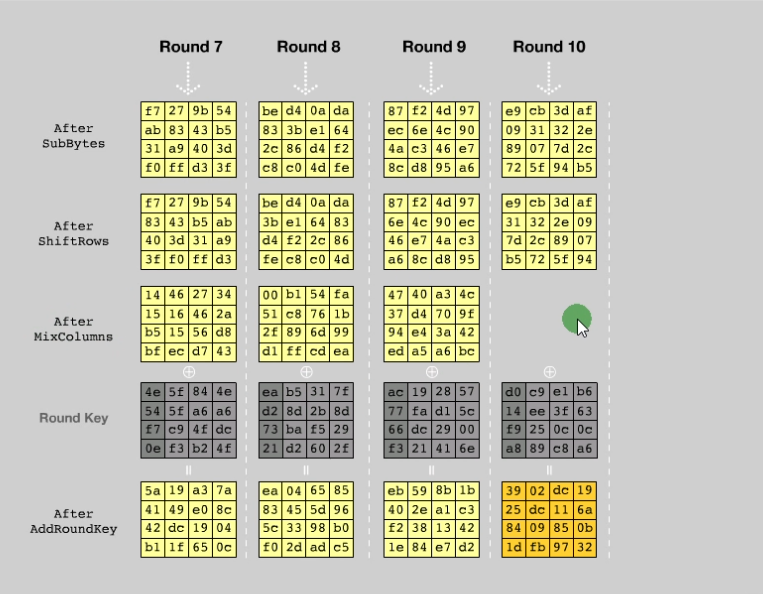
9轮运算
1 | sbox替换 |
末运算
1 | sbox替换 |
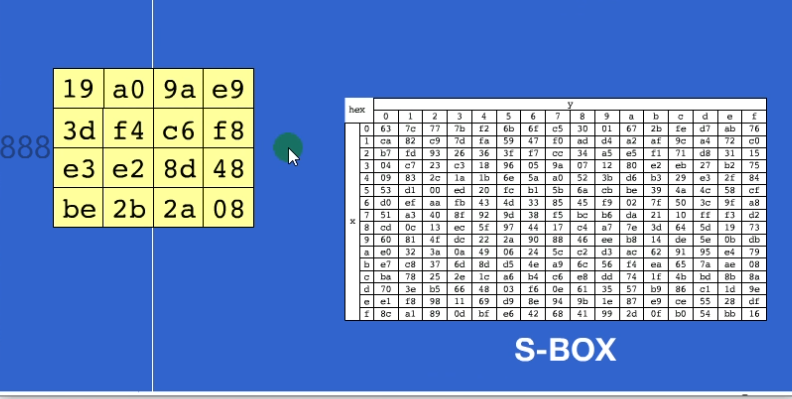
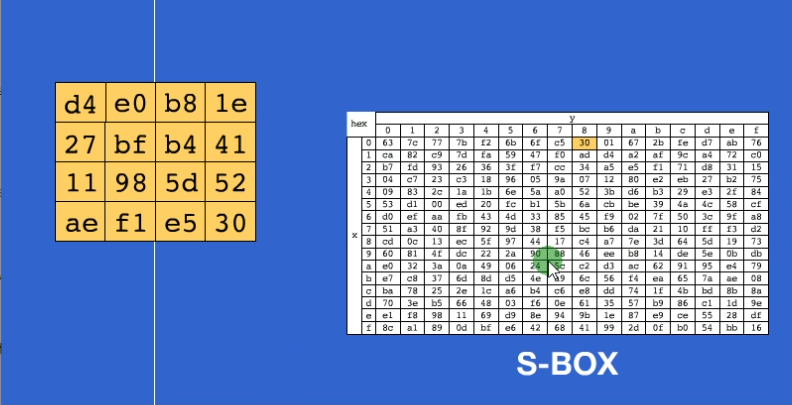
sbox运算
就是从sbox里面去取对应的值,比如说这里的state里的19,找sbox里的第一行第九列,就是d4…以此类推
完毕之后如下
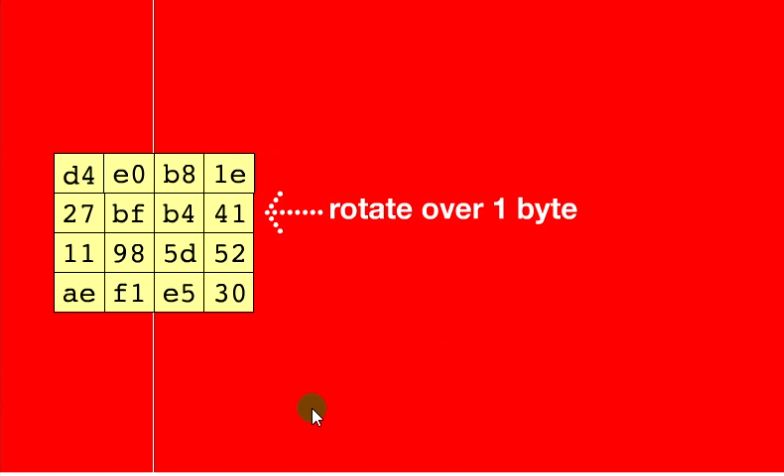
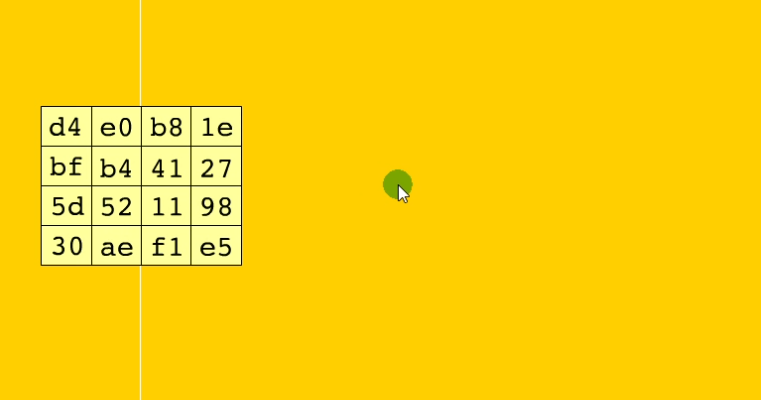
循环左移
行方向上移动,第一行不动,第二行左移1个字节,第三行左移2个字节,第三行左移3个字节
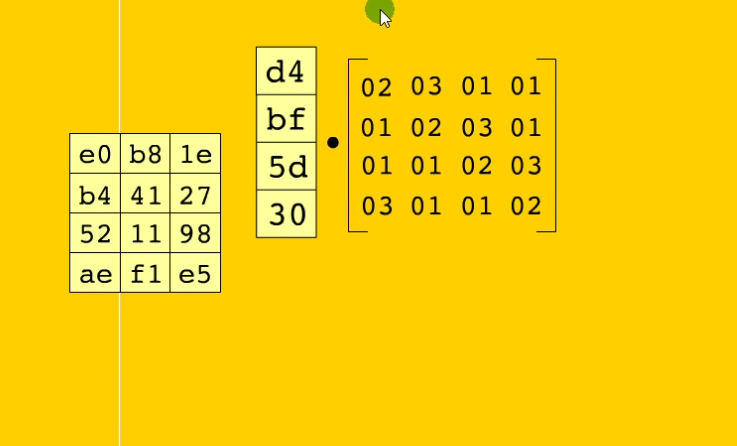
列混淆
不用管,纯数学,就是矩阵乘法,只需要知道特征就行,会存在一个4*4数组,里面就是02 03 01这种数字
数据如果有溢出的话,需要做另外的计算,就是用到GaloisMultiplication的乘法运算(0x1B 0x80),需要与0x1B进行位与,就是有0x1B和0x80这两个数字
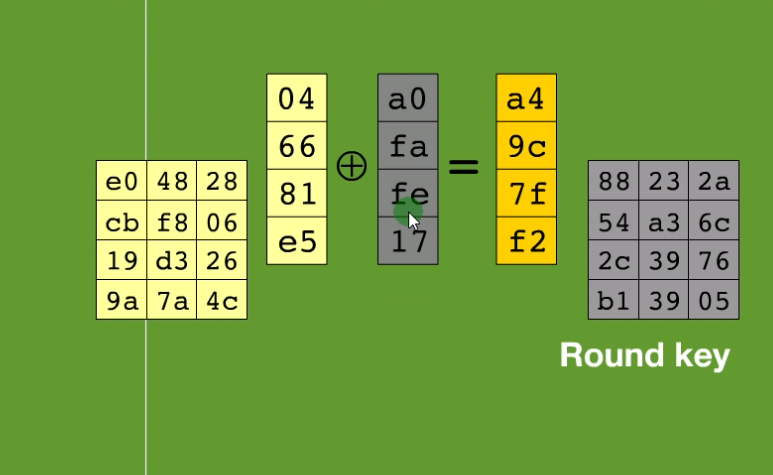
AddRoundKey
就是每一列进行异或,得到新的
当然这里的RoundKey每轮不一样,总共有9轮,如下所示
S盒与逆S盒
DES里有8个S盒,加解密用的同一个S盒
AES里只有2个,加密用一个,解密用一个,互为可逆的
推几个就很明显了
1 | // S盒 |
循环左移的几种实现
就是把比特位左移改了一下
1 | // uint32_t x循环左移n位 |
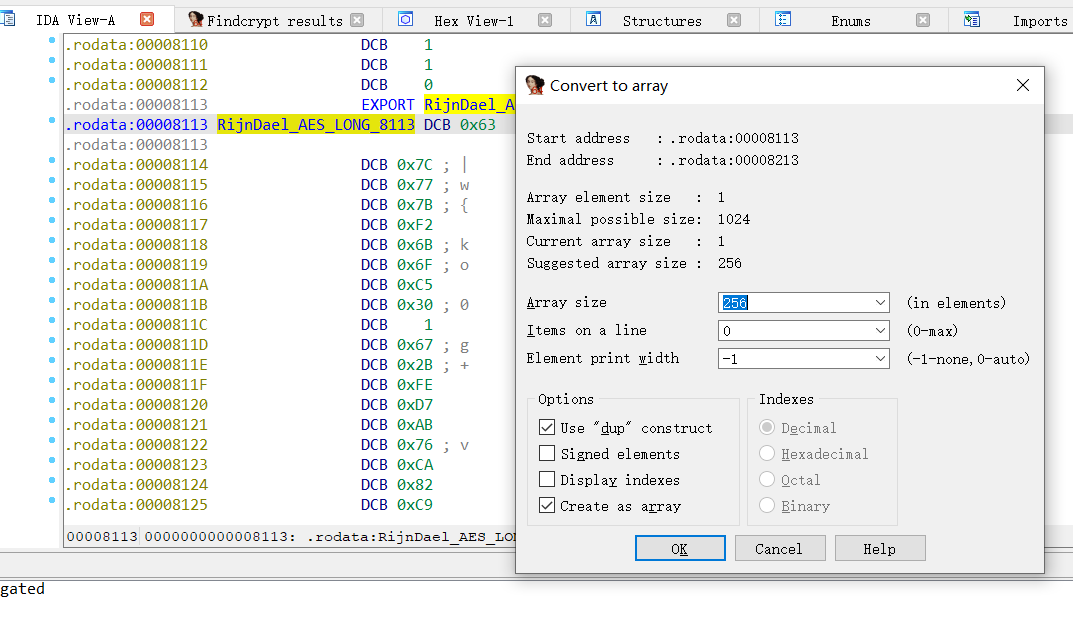
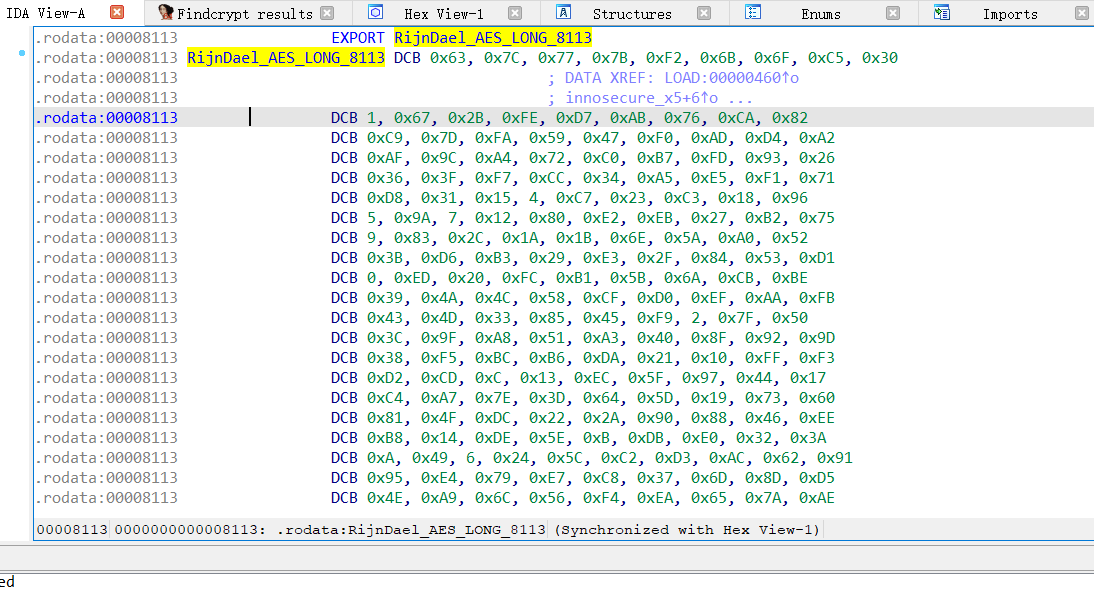
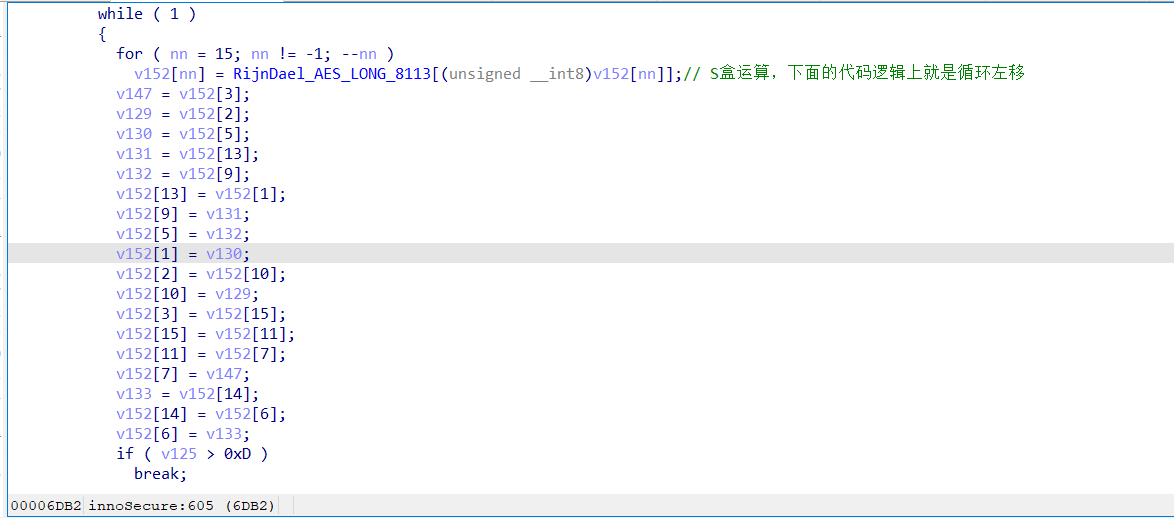
IDA里的另一种实现,是libInnoSecure.so的实现
找到数据,进入
右键数组名,选择Byte 0x63,再次右键选择array,array size是256,可以看出来是个数组了
随便找一下引用
推一下下标就知道了
1 | 原来state的排序是(数字就是序号) |
个人感觉就看一下下标的特征就行了,1 5 9 13这些
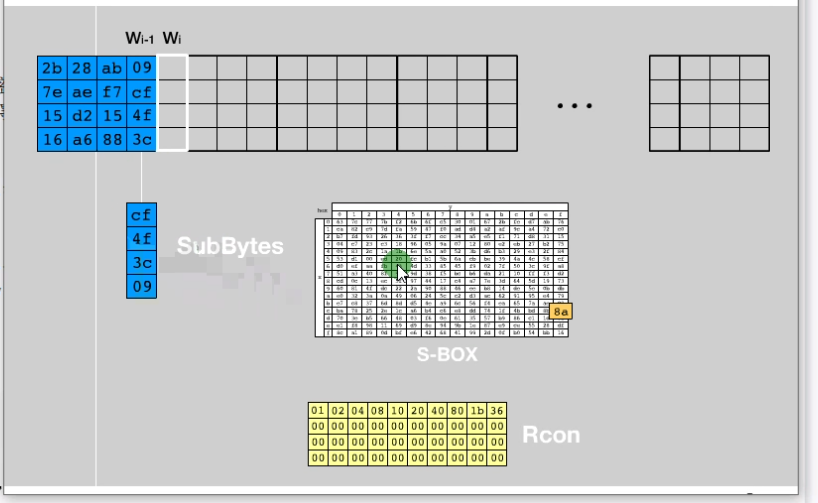
密钥的编排
种子密钥state操作之后每列分为W0-W3
将种子密钥扩展,得到W0-W43
1 | Wi = Wi-1 ^ Wi-4 (如果下标不是4的倍数) |
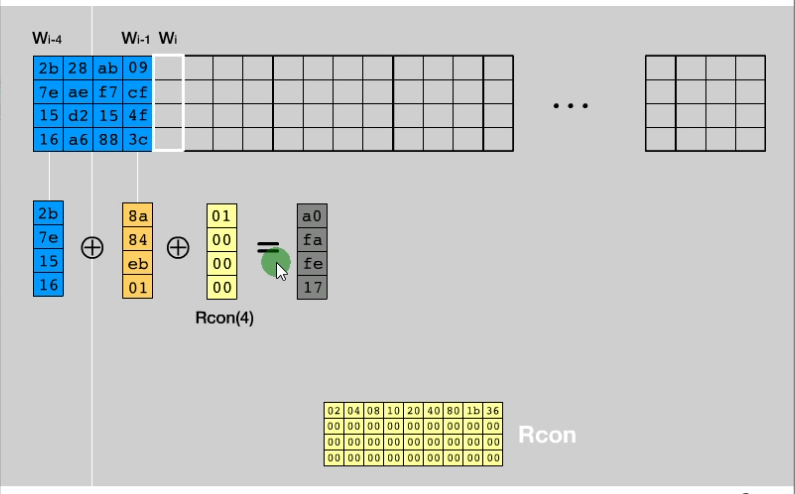
T函数流程:循环左移1个字节、S盒替换、与Rcon异或,例如:取出W3,进行移位,然后再把移位之后的结果和S盒进行替换,再与Rcon进行异或,得到中间结果,再和W0异或,结果放到W4这里
Rcon的下标和i也有关系,比如要计算W8,那么就是和Rcon[8]进行计算
一共是W0-W43,一共44组,每轮使用4组(也就是4*4的假矩阵)
其他注意
字节替换和循环左移是可以换顺序的
第一次对明文进行AddRoundKey的时候,因为那里是直接和种子密钥进行异或,在异或处可以得到种子密钥,而且如果是ECB模式的话,还能得到明文,所以在这里Hook异或的代码,就可以拿到种子密钥,当然前提是代码是标准AES算法,如果是AES查表法实现,是没有AddRoundKey的
AES的代码实现
1 |
|
AES查表法的实现
思路,明文不管怎么经过S盒替换,产生的结果一定是有限个的,所以列混合之后的结果一定也是有限的
查表法就是把这些有限的值全部写死
查表法的核心思想是将字节代换层、ShiftRows层和MixColumn层融合为查找表:每个表的大小是32 bits(4字节)乘以256项,一般称为T盒(T-Box)或T表。加密过程4个表(Te),解密过程4个表(Td),共8个。(也不一定是8个,还有各种可能)
推导过程参考https://zhuanlan.zhihu.com/p/42264499,不过看了也看不懂,反正结论如下
每列密文都经过了4个T表的查表(就是T函数),然后和本轮子密钥 ki 异或,一共异或了5次
上面图里的A0-A15是16个元素的序号
rust实现的代码
1 | // round 2 to round 9 (or 11, 13) |
代码解释:
上面的原理可以看到,D0-D3这一列的结果是要依次取出A0、A5、A10、A15,然后分别查表,把查表的结果异或之后再与子密钥异或
怎么取A0到A15呢?以这一句为例
1 | wa0 = TE0[ (wb0 >> 24) as usize ] ^ TE1[((wb1 >> 16) as usize) & 0xFF] ^ |
假设A0-A15如下
1 | wb0 0 4 8 12 |
当然,由于最后一轮没有列混淆操作,所以有时候还需要查一个SBOX表(S盒),但是也不一定需要S盒,比如openssl里就是4个T表搞定的,T表里的某个字节就是S盒里的元素,所以S盒也省了
1 | // final round |
openssl的AES实现
一般Android上,查表法会比较多
1 | https://github.com/openssl/openssl/blob |
从T表里定位出S盒的元素
1 | int AES_set_encrypt_key(const unsigned char *userKey, const int bits, |
解密的时候还是定义的逆S盒,因为逆S盒从T表里取不出来
查表法的还有一个特征就是5次异或、4次异或等
/* round 1: */
t0 = Te0[s0 >> 24] ^ Te1[(s1 >> 16) & 0xff] ^ Te2[(s2 >> 8) & 0xff] ^ Te3[s3 & 0xff] ^ rk[ 4];
t1 = Te0[s1 >> 24] ^ Te1[(s2 >> 16) & 0xff] ^ Te2[(s3 >> 8) & 0xff] ^ Te3[s0 & 0xff] ^ rk[ 5];
t2 = Te0[s2 >> 24] ^ Te1[(s3 >> 16) & 0xff] ^ Te2[(s0 >> 8) & 0xff] ^ Te3[s1 & 0xff] ^ rk[ 6];
t3 = Te0[s3 >> 24] ^ Te1[(s0 >> 16) & 0xff] ^ Te2[(s1 >> 8) & 0xff] ^ Te3[s2 & 0xff] ^ rk[ 7];
/* round 2: */
s0 = Te0[t0 >> 24] ^ Te1[(t1 >> 16) & 0xff] ^ Te2[(t2 >> 8) & 0xff] ^ Te3[t3 & 0xff] ^ rk[ 8];
s1 = Te0[t1 >> 24] ^ Te1[(t2 >> 16) & 0xff] ^ Te2[(t3 >> 8) & 0xff] ^ Te3[t0 & 0xff] ^ rk[ 9];
s2 = Te0[t2 >> 24] ^ Te1[(t3 >> 16) & 0xff] ^ Te2[(t0 >> 8) & 0xff] ^ Te3[t1 & 0xff] ^ rk[10];
s3 = Te0[t3 >> 24] ^ Te1[(t0 >> 16) & 0xff] ^ Te2[(t1 >> 8) & 0xff] ^ Te3[t2 & 0xff] ^ rk[11];
...
openssl的EVP使用
以librong360.so为例
可以看到导入表里很多函数,当然这里插件是找不到加密的,因为so自己没实现这个算法,是用的别的so里的
图1
以EVP_aes_128_cbc函数为例,找到调用的地方
1 | char *__fastcall cbc_encode(int a1, int a2, _DWORD *a3, int a4) |
白盒AES算法
白盒AES的核心是直接把key融入到一个表中,这样AES算法就变成了一个查表的过程,这样攻击者很难拿到原始的key,有160个表,160个表拿到没问题,但是不好拿到密钥
但是加密结果和AES一致
AES和DES的区别与联系
DES和AES都是对称加密算法,加解密使用同一个密钥
DES和AES都是分组加密算法,DES的分组长度是64bit,AES的分组长度是128bit
DES密钥64bit,AES密钥128、192、256
DES运算的基本单元是bit,AES的基本运算单元是字节
DES和AES都可以分成密钥的编排和明文的处理
DES和AES在密钥的编排中,都通过对密钥的处理生成一系列的子密钥subkey,每轮运算用1个
DES有16轮运算,在密钥编排中生成了16组子密钥;AES有10、12、14轮运算,也生成10、12、14组子密钥,两者都是每轮用一个
AES每轮运算经过4个步骤
1 | 第一步字节替换(S盒替换),16*16的S盒,加解密使用不同的S盒 |
PS几点
对于概念性,原理性的东西知道即可,重点是要熟悉哪些特征是哪些算法
看到一些常量,也可以直接去搜这些常量,看能不能找到算法